We work in the complex plane and without loss of generality we assume the charges are placed at the locations
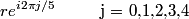 The electric field at the center is then given by Coulomb's Law: 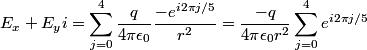 We use the following formula for a geometric series: 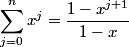 where 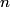 is a positive integer and is a positive integer and  is any complex number not equal to 1. Letting is any complex number not equal to 1. Letting 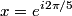 and and 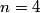 , we find that , we find that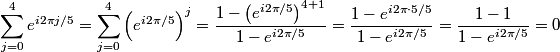 Therefore, 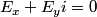 at the origin. Therefore, 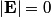 at the origin. Therefore, answer (A) is correct. at the origin. Therefore, answer (A) is correct. |
Please send questions or comments to X@gmail.com where X = physgre.